DDC-43: Vector norm and vector dimension

A data challenge a day helps you master machine learning

About these daily data challenges

Each post is an exercise that helps you learn about data in Python.

Try to solve the exercise before checking my solution at the bottom of the post 🤓

You can share your solution or visualization in the comments!

Today’s challenge

Some linear algebra terms:

• Vector: an ordered list of numbers, e.g., [1,3,-12]

• Vector norm: The square root of the sum of its squared elements. You can calculate the vector norm using np.linalg.norm

• Vector dimensionality: The number of elements in the vector, e.g., 3 in the vector above.

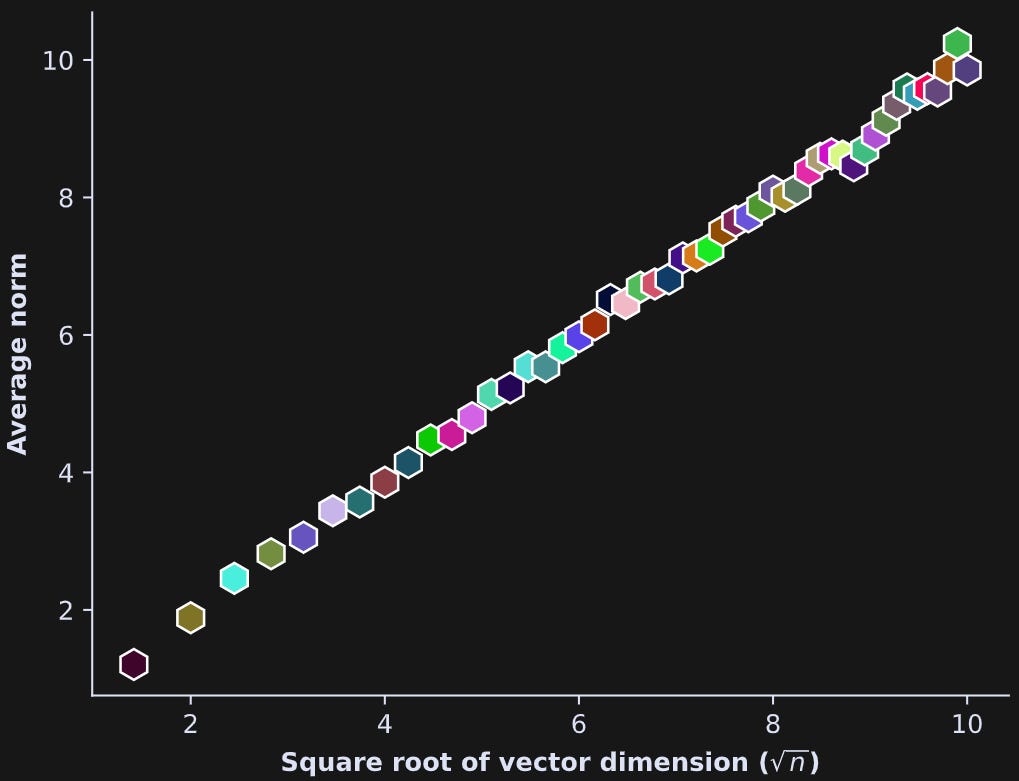
Your goal here is to demonstrate that the expected norm of a random-number vector equals the square root of its dimensionality.

Create 50 vectors of Gaussian random numbers of dimensionality = 2, calculate the norm of each of the 50 vectors, and average those norms together. Then repeat that for dimensionalities from 2 through 100 in steps of 2. Plot the average norm by the square root of the dimensionality, as shown below.

I set the color of each hexagon to be a randomly generated RGB code.

.

.

.

.

Scroll down for the solution…

.

.

.

.

.

.

.

.

keep scrolling!

.

.

.

.

import numpy as np
import matplotlib.pyplot as plt

vector_dims = np.arange(2,101,2)
n_repeats = 50

for i,m in enumerate(vector_dims):
  matrix = np.random.randn(m,n_repeats)
  norm = np.linalg.norm(matrix,axis=0).mean()
  plt.plot(np.sqrt(m),norm,’wh’,markersize=12,
           markerfacecolor=np.random.rand(3))

plt.gca().set(xlabel=’Square root of vector dimension ($\\sqrt{n}$)’,
              ylabel=’Average norm’)
plt.show()