DDC-51: Distributive property of vector-scalar multiplication

A data challenge a day helps you master machine learning

About these daily data challenges

Each post is an exercise that helps you learn about data in Python.

Try to solve the exercise before checking my solution at the bottom of the post 🤓

You can share your solution or visualization in the comments!

Today’s challenge

Demonstrate the distributive property of vector addition and scalar multiplication. The distributive property states the following, for some scalar \alpha and two vectors v_1 and v_2.

Using the following vectors and scalar, show that both sides of the equation above and equal.

v1 = np.array([ 1,2,-3 ])
v2 = np.array([-5,1.5,3 ])
s  = 2.5

.

.

.

.

Scroll down for the solution…

.

.

.

.

.

.

.

.

keep scrolling!

.

.

.

.

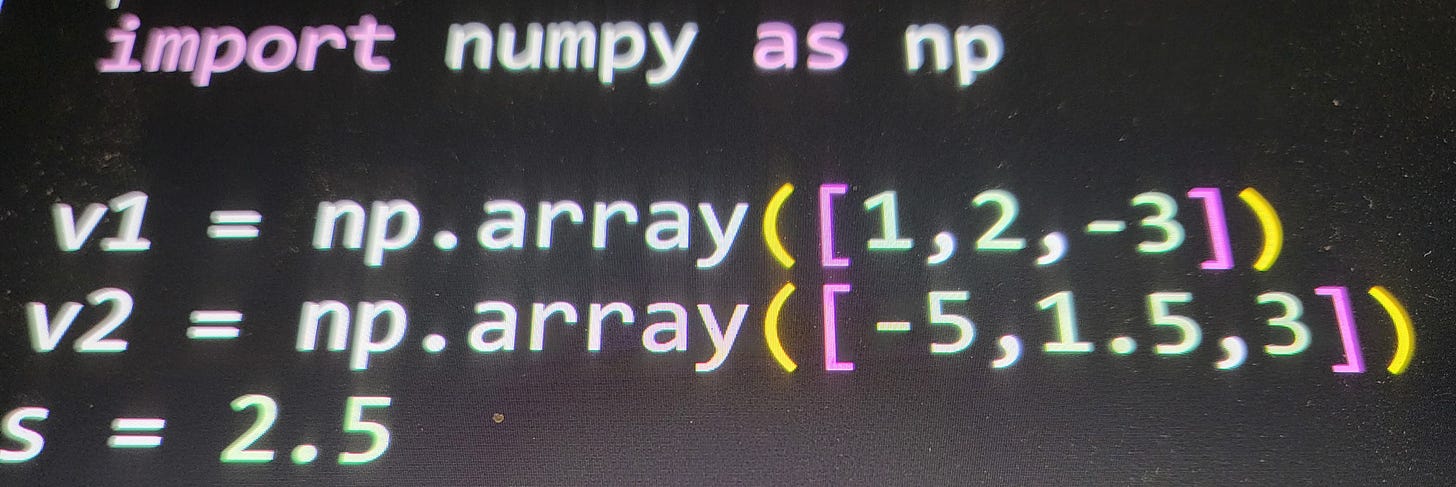
import numpy as np

v1 = np.array([1,2,-3])
v2 = np.array([-5,1.5,3])
s = 2.5

result1 = s*(v1+v2)
result2 = s*v1 + s*v2
print(result1,’\n’,result2)