DDC-54: Eigenvalues and squared singular values
A data challenge a day helps you master machine learning
About these daily data challenges
Each post is an exercise that helps you learn about data in Python.
Try to solve the exercise before checking my solution at the bottom of the post 🤓
You can share your solution or visualization in the comments!
Today’s challenge
Create matrix S using the equation below. Extract its singular values using the SVD, and its eigenvalues using eigendecomposition. Show that the squared singular values equal the eigenvalues. You might need to sort the eigenvalues.
.
.
.
.
Scroll down for the solution…
.
.
.
.
.
.
.
.
keep scrolling!
.
.
.
.
import numpy as np
M = np.random.randn(4,10)
S = M@M.T
eigenvalues = np.linalg.eig(S)[0]
singularvals = np.linalg.svd(M)[1]
np.sort(eigenvalues)[::-1],singularvals**2
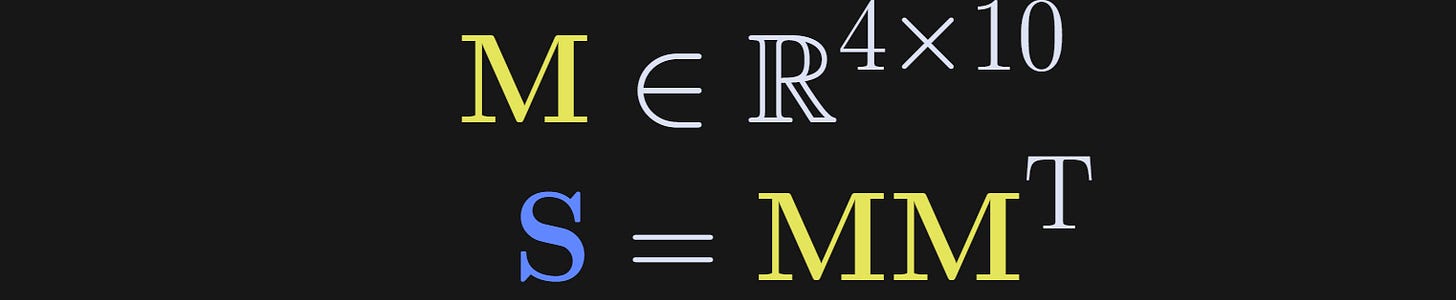

Hiiii, a little bit different, here is my solution:
# DDC-54: Eigenvalues and squared singular values
import numpy as np
rng = np.random.default_rng(seed=42)
M = rng.integers(low=0, high=101, size=(4, 10))
S = M@M.T
U,Sing, Vh = np.linalg.svd(S)
Sing_s = np.sort (Sing)
eigen_S, V = np.linalg.eig (S)
eigen_S_sorted = np.sort(eigen_S)
are_equal_approximately = np.allclose(Sing_s, eigen_S_sorted)
print("Sing_s :", Sing_s)
print("eigen_S_sorted:", eigen_S_sorted)
print(f"\nAre they approximately equal? {are_equal_approximately}")