The Fourier transform, explained with for-loops

How small waves make Big Waves

Who was Fourier and what did he transform?

Joseph Fourier was a French physicist, mathematician, and inventor of Cirque du Soleil (ok, just kidding about that last one). He had the radical idea of using sine waves to represent any mathematical function. That might sound trite nowadays, but it really was a radical idea at the time, and widely rejected.

But Fourier got the last laugh. His idea transformed engineering, telecommunications, signal processing, image processing, and basically everything in modern computing and information technologies.

The Fourier transform (FT) has beautiful nuances and complexities when you get into the details of it, but my goal in this post is to present its essential form using code, for-loops, and visualizations.

Time and frequency domains

The time and frequency domains are two different ways of looking at a signal. It might seems surprising at first, but the two panels below show the same signal represented in different ways.

Figure 1: A signal can be represented in the time domain (left) or in the frequency domain (right). The information is the same, but the two domains have complementary advantages and limitations.

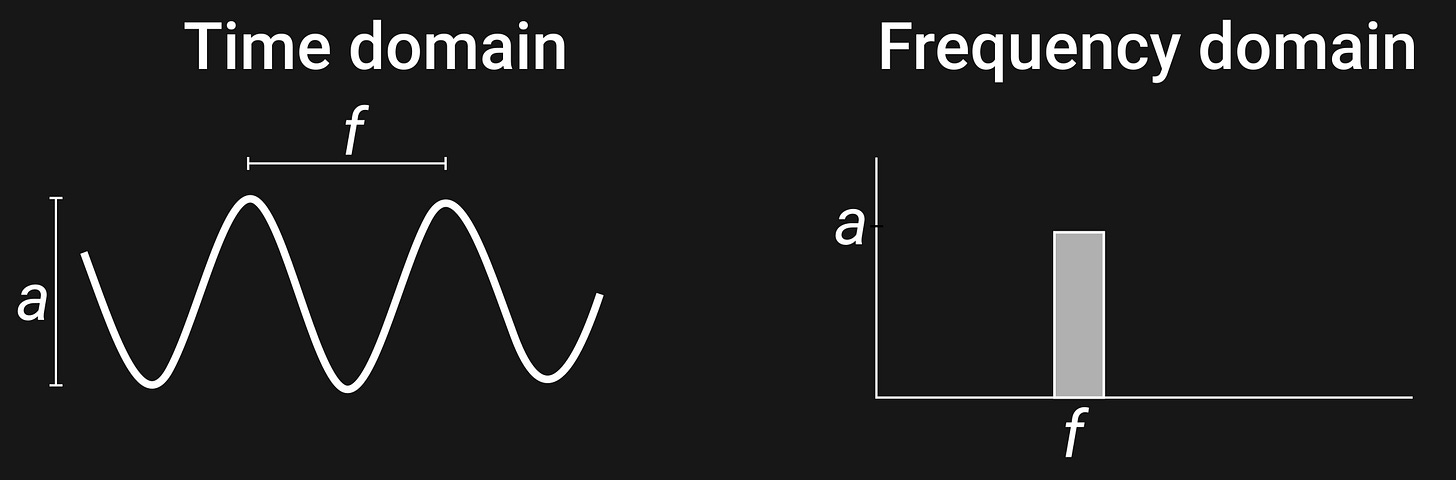
To create a frequency-domain representation, measure the vertical distance between the trough and the peak (“a” in the graph), and plot that number (the “energy” of the signal) as the height of a bar on the y-axis, at the x-axis location corresponding to the distance between each successive peak in the time-domain signal (“f” in the graph).

In other words, the time domain shows how the signal unfolds over time, whereas the frequency domain shows how the signal can be separated into rhythmic components.

Example of the Fourier Transform (FT)

(As always in my posts, you can find the complete Python notebook file to reproduce and extend these figures and code blocks here on my github.)

Check out the signal below; I created it by combining several sine waves. Here is a question for you: How many rhythmic components are in this signal? What are their frequencies (speeds) and how strong (amplitude) is each component?

Figure 2: A compound signal comprising multiple simpler signals.

You really can’t tell just from the combined signal. Obviously it’s rhythmic, but exactly which rhythms are in there is difficult to determine — and I haven’t even added noise to the signal, which would only complicate things.

The figure below shows where that signal came from. The left column shows four sine waves of different frequencies (Hz) and amplitudes (a). The top-right panel shows the signal resulting from summing those four signals together (same as above).

Figure 3: Building up a composite signal from simpler sine waves, only to deconstruct it using the Fourier Transform.

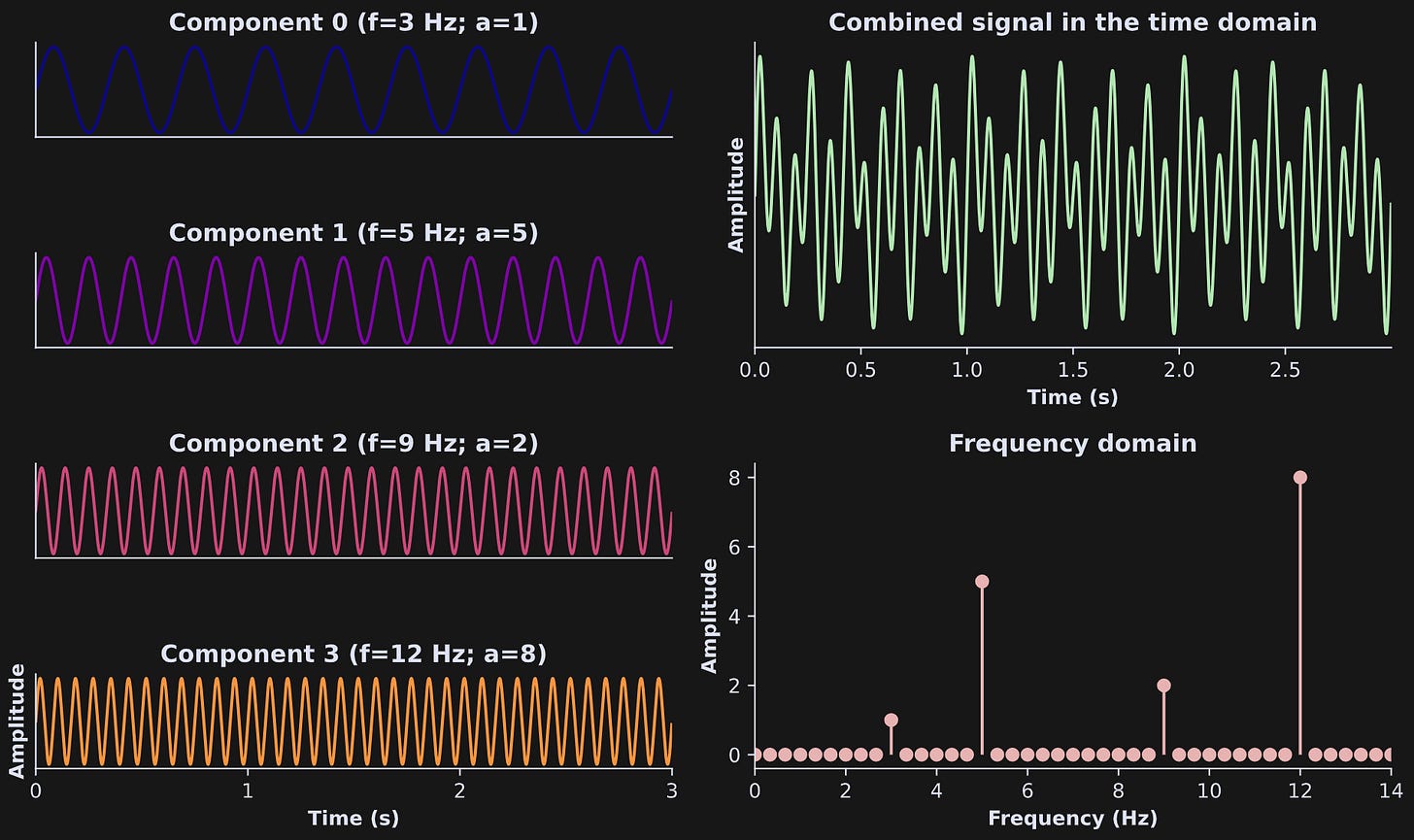
The lower-right panel is the amplitude spectrum. Notice that the non-zero stems clearly reveal the frequencies (x-axis) and amplitudes (y-axis) of each component.

The goal of the rest of this post is to use for-loops in code to explain how that plot is created.

Dot products with sine waves

Let’s start our adventures into Fourierland by creating a signal (different from the ones above) and calculating the dot product between that signal and a collection of sine waves.

As a reminder: The dot product is a simple yet powerful mathematical operation that produces one number from two vectors, and is defined as element-wise multiplication and sum. For example, given the vectors v=[1,2,3] and w=[3,0,4], the dot product <v,w> = 1*3 + 2*0 + 3*4 = 15. The dot product is the foundational computation underlying correlation, convolution, template-matching, filtering, PCA, artificial neural networks, ChatGPT, and, like, a zillion other applications of math.

Here’s our signal (as in all of my posts, only the essential code is presented here; I recommend downloading or at least looking at the full code notebook):

Figure 4: A signal made from a sine wave and a Gaussian taper.

This signal is defined as a sine wave at 5 Hz multiplied by a Gaussian. It has a specific name — Morlet wavelet — although that’s not relevant here. The θ (variable theta) term shifts the signal’s phase; notice that it’s kind of wobbly around t=0. That will be important in a moment.

Now what I’m going to do is generate some cosine waves (just the cosines; no tapering functions), and calculate the dot product between each of those waves and the signal. This is not a FT, but it is like the primordial ancestor from which the FT evolved.

Figure 5: Left panel shows the same signal as in Figure 4. Right panel shows the amplitude spectrum, generated by calculating dot products between the signal and “template” cosine waves at the x-axis frequencies.

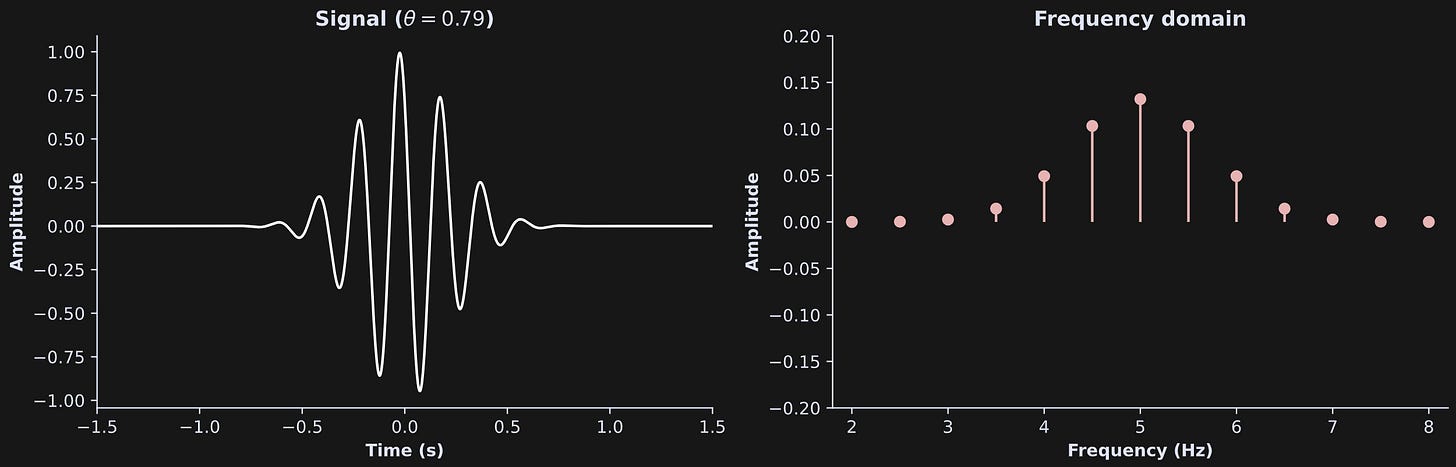
The left panel shows the signal again. The right panel shows how much “energy” is in the signal at each of the frequencies I tested. That amplitude spectrum peaks at 5 Hz and tapers down on both sides. The smooth decays on either side of 5 Hz reflect the changes in the signal over time — only pure sine waves in the time domain can have perfect spikes in the frequency domain. Temporal dynamics (a.k.a. non-stationarities) in the time-domain signal are captured by energy at other frequencies.

In the code, the dot product is divided by the number of points. That’s not part of the dot product formula, but it is part of the FT. Well, sort of. If you want the resulting amplitude spectrum to have the same units as the original signal, then you divide by N. The dot product is a big summation, and so the amplitudes can grow arbitrarily large with signal length; dividing by N is like turning the sum into an average. It’s also conceptually similar to scaling by dx in an integral.

But there’s a problem

The problem is a phase-dependency between the signal and the sine wave. Check out what happens when I set theta = 2*np.pi/4 and re-run the code above.

Figure 6: Same as Figure 5 but with a slightly different phase offset value for the signal.

Hmm, now it looks like the signal has NO ENERGY at all! That’s obviously wrong. Here’s an even more striking result of setting theta = 3*np.pi/4

Figure 7: Same as Figure 6 but a different phase parameter.

Negative energy?! What does that mean? Nothing, actually; it has no physical interpretation. The problem here is phase-dependency between the signal and the sine waves: Depending on the relative phases between the signal and the sine wave, the dot product can be positive, negative, or zero.

Figure 8 below illustrates this in more detail. The white sine wave is at 5 Hz, and the three colored lines show the same signal but different θ values. The legend shows the dot product (dp) for each signal with the same sine wave.

Figure 8: Illustrating the phase-dependency of dot products with sine waves.

That’s quite striking, because the signal frequency and Gaussian envelope are identical. But the phase (mis)alignments are a problem: We want the FT to tell us how much energy is in a signal at a given frequency, regardless of where the signal just so happens to align with the sine wave.

Enter the complex sine wave.

Complex sine waves

A complex-valued sine wave is a sine wave and a cosine wave put together. Not summed, or multiplied, but entangled into a helix.

A complex sine wave is created by setting the real part to be a cosine and the imaginary part to be a sine, which can be compactly written using one of Euler’s great identities (all of Euler’s identities are great, but this one is perhaps the greatiest) (i is the imaginary operator, defined as the square root of -1).

In code, it looks like this: comp_sinew = np.exp( 1j*2*np.pi*frex*time )

You can visualize a complex sine wave as two separate waves on the same 2D axis, or in a 3D plot with time on the x-axis, the real part (corresponding to a cosine) on the y-axis, and the imaginary part (corresponding to a sine) on the z-axis.

Figure 9: Complex sine waves in 2D and in 3D.

How do complex sine waves solve the phase-dependency problem? Because any phase dependence can be expressed as some combination of cosine and sine, and therefore repeating the dot product with a cosine and a sine allows us to calculate the true relationship between the signal and the sines, without worrying about the phase dependency.

This means that we can repeat the for-loop with dot products, but using complex-valued sine waves instead of real-valued cosine waves. Each dot product is complex-valued, and the feature we extract is its magnitude, which is the distance to the origin. I’ll unpack that in a moment, but first, please inspect the figure below, which shows the dot product magnitudes from the same sine wave frequencies and theta value as in the last analysis from the real-valued cosine waves.

Figure 10: Dot products with complex sine waves are robust to phase shifts.

I won’t show any other values of theta because the right-hand plot looks identical, but of course you can check my claim in the online code.

Let’s visualize the phase dependency in a more visually enticing way. The figure below shows 16 signals that differ only in the θ parameter (left panel), the dot product amplitude spectrum with real-valued cosines (middle panel), and the same spectrum with complex-valued sine waves (right panel). The complex sine waves are completely robust to the phase of the signal. In other words, combining real-valued cosines and imaginary-valued sine waves allows us to quantify the amount of energy in the signal at each frequency, regardless of the relative phase differences.

Figure 11: Complex sine waves completely resolve the phase dependency. (I added small x-axis shifts in the right-side plot to facilitate visual inspection.)

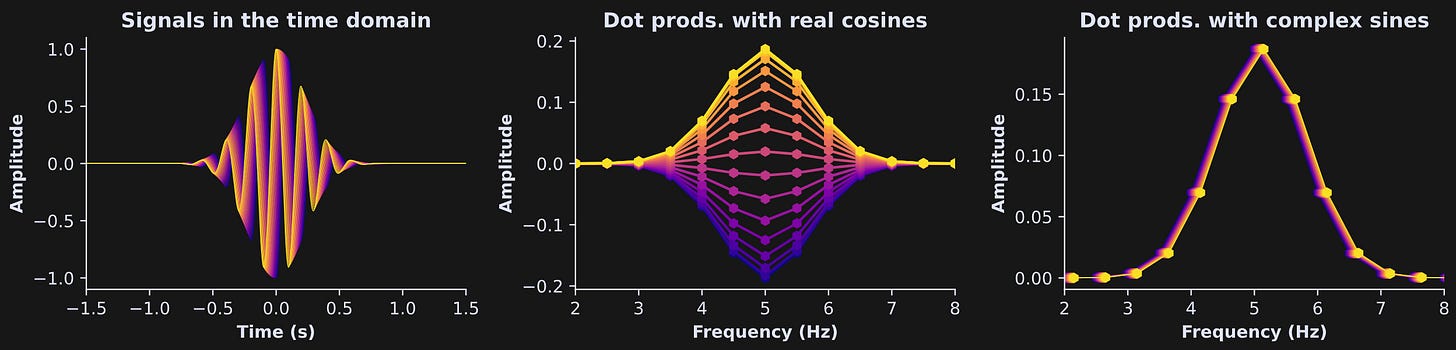
But why does that happen? Consider that a dot product between the (real-valued) signal and the real-valued cosine is itself a real-valued number. It exists somewhere on the number line. That’s what you see in the left panel below.

Figure 12: Real-valued dot products (left panel) lack the dimensionality to handle phase differences. Complex-valued dot products (right panel) come to the rescue.

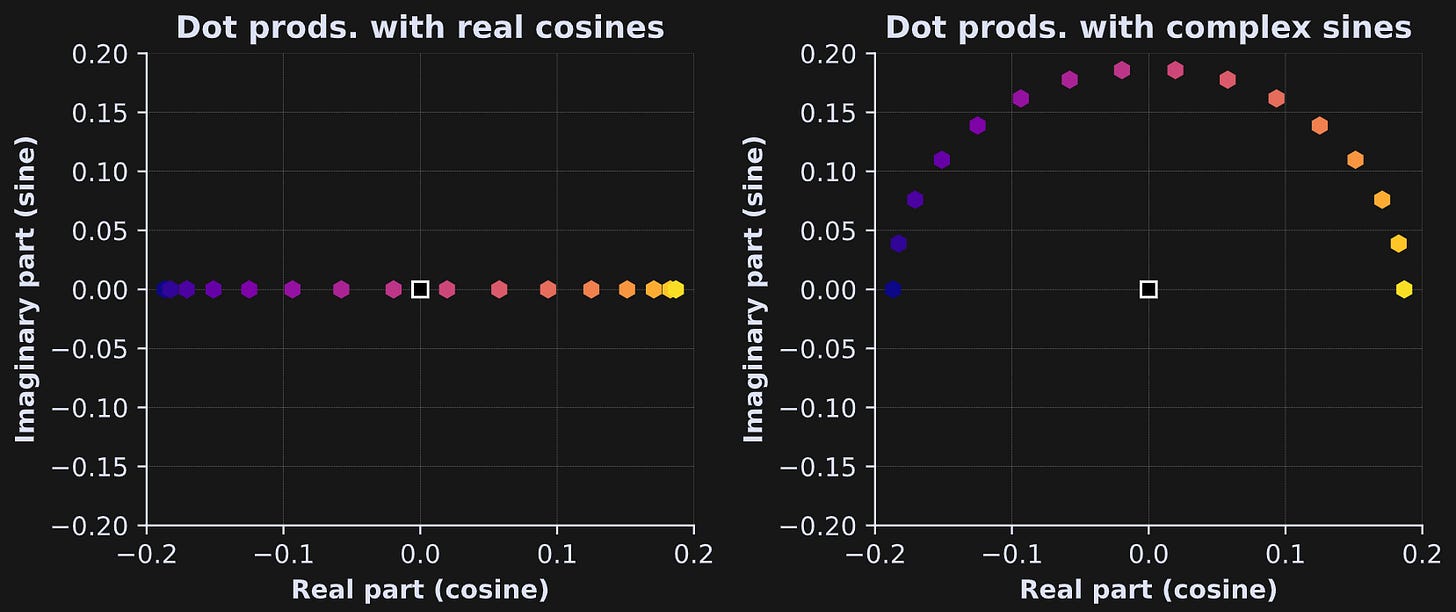
The color of each dot corresponds to the θ value from the previous figure. The phase offsets cause the relationship with the cosine to vary between negative and positive.

Now consider that the dot product between the signal and complex-valued sine wave is a complex number. The phase differences will make the signal look more like a cosine, more like a sine, or something in between. But the distance to the origin is the same, even as the phase changes. That’s what the right-hand panel in Figure 12 shows. You can also see that projecting each complex dot product down to the x-axis would recreate the real-valued result in the left panel.

The full FT in a for-loop

The actual FT is basically the same as the for-loop with a complex-valued signal. There are some nuances that I haven’t yet discussed, including:

1. The time vector for the sine waves is normalized to [0,1]. That normalization allows us to use the same algorithm for any regularly sampled signal of any sampling rate.

2. The number of frequencies is the same as the number of sample points. So if your time series signal is 1234 points long, you use 1234 complex sine waves. Having the same number of frequencies as time points allows the transformation to be perfect (lossless).

3. Half of those frequencies are called “positive” and half are called “negative.” The amplitudes in the signal are split between the positive and negative frequencies — that’s why I’ve been multiplying the dot products by 2. The brief explanation is that to represent a real-valued sine wave using complex-valued sine waves, you need a conjugate pair (r is some real number):

   

4. If the signal is real-valued, then the amplitude spectrum is symmetric, so in practice, people ignore the negative frequencies and double the positive frequencies.

Here’s the code!

And that’s it! One of the most important transformations in all of digital telecommunications is just a for-loop with two lines (which you could even reduce to one line).

Each “Fourier coefficient” is just a dot product. We call it a Fourier coefficient to honor Fourier’s myriad important contributions to humanity, but it’s just a regular ol’ dot product.

Because the time vector used in the FT is unit-normalized, the frequencies are also normalized. To interpret the frequencies in units of Hz (1/s), we multiply the normalized units by the sampling rate. But because the positive and negative frequencies mirror each other (and other nuances related to Nyquist theory that I’m smoothing over here), we only consider the positive frequencies, which are those between 0 and Nyquist.

Now we can visualize the full amplitude spectrum:

Figure 13: The full FT of the signal.

Not surprisingly, it looks a lot like the amplitude spectra I showed earlier in this post. I really shouldn’t call those previous results “Fourier spectra,” but they did encapsulate the key ideas of the FT.

The fast Fourier Transform (FFT)

In practice, you don’t run a for-loop to implement the FT. It’s slow and clunky, and computers can implement the FT faster and more efficiently. There is an algorithm (actually, a small family of related algorithms) called the fast Fourier Transform, and that’s what you use in practice.

F = np.fft.fft(signal) / len(signal)

That variable F is exactly identical to the variable fourierCoefs from my for-loop. The following figure doesn’t exactly prove that they’re always the same, but I hope you find it compelling.

Figure 14: The output of fft() matches the for-loop FT.

When should you use the loop-based FT?

NEVER!!

Well, OK, that’s a bit dramatic. There are two scenarios in life when you should prefer the loop-based FT over the FFT.

1. Right here, right now, when learning about the mechanics of the FT.

2. When you are teaching someone else about the mechanics of the FT.

In other words, the loop-based FT has exceptionally high educational value, but no application value. Why not?

Because it’s really slow. For real-world applications with very long signals, the fft() function might take a few seconds while the loop implementation might take hours. Computer scientists have been refining FFT algorithms for decades, and once you understand how the FT works, it’s best to rely on their decades of brilliant and diligent work.

That’s the essence

There’s so much more to know about the FT, like how many frequencies you can use, why it’s a lossless transformation, the weirdness about “positive” vs. “negative” frequencies, interpreting the phase spectrum, the meaning of the DC and Nyquist frequencies, extensions to 2D (for image processing applications), and so on.

If you’d like to learn more, you can consider taking my 8-hour video-based FT course (I additionally provide MATLAB code in that course).

Thank you for reading 🤗

I hope you’re finding my Substack posts helpful and interesting. Maybe you even did that quick-nose-exhalation thing that people do when they read something funny but not that funny.

I wrote this post for you. And I have time to write it for you because last month, a bunch of curious and supportive people bought my courses and/or my books, or supported me here on Substack, and that paid me enough royalties that I don’t need to beg The Man for a paycheck. Are you also curious and supportive?